Understanding Coulomb’s Law:
Coulomb’s law describes the electrostatic force between two charged particles. It states that the force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. Mathematically, Coulomb’s law can be expressed as:

Where:
- 𝐹 is the electrostatic force between the charges,
- 𝑞1 and 𝑞2 are the magnitudes of the charges,
- 𝑟 is the distance between the charges, and
- 𝑘 is Coulomb’s constant, approximately 8.9875×10^9 N⋅m^2/C^2.
This law helps explain how charged particles interact and is fundamental in understanding various phenomena in electromagnetism.
Related Sample Questions:
Here are some questions :
- Two point charges, +q and -2q, are placed 3 meters apart on the x-axis. What is the magnitude and direction of the electric field at a point on the y-axis located 4 meters away from the midpoint between the charges?
- Three point charges, +2q, -q, and +3q, are placed at the vertices of an equilateral triangle with sides of length ‘a’. What is the net electric force on the charge +2q?
- A charge of magnitude q is placed at the origin, and another charge of magnitude 2q is placed at (3,4). Determine the electric field at the point (5,0).
- Four identical charges, each with a magnitude of +q, are arranged at the corners of a square of side length ‘a’. What is the electric potential at the center of the square?
- A charge q is placed at the origin, and a charge -2q is placed at (4,0). Find the point on the x-axis where the electric field due to these charges is zero.
- Consider two charges, +q and -2q, separated by a distance ‘d’. At what point on the line connecting the charges is the electric potential zero?
- Three charges, +2q, -3q, and +q, are arranged in a straight line with equal spacing between them. Determine the point(s) along this line where the electric field is zero.
- A charge +3q is located at (0,0), and a charge -2q is located at (-3,4). Find the point on the x-axis where the electric potential is maximum.
- Four charges, +q, -q, +2q, and -2q, are placed at the corners of a square with sides of length ‘a’. What is the net electric field at the center of the square?
- Two charges, +q and -2q, are located on the y-axis at (0,a) and (0,-a) respectively. Determine the point(s) on the x-axis where the electric potential is zero.
Sample Answer:
Let’s Consider question number 4.
Four identical charges, each with a magnitude of +q, are arranged at the corners of a square of side length ‘a’. What is the electric potential at the center of the square?
Solution:
To solve this problem, we need to calculate the electric potential at the center of the square due to each individual charge and then sum up these potentials.
Given:
- Four identical charges, each with a magnitude of +q.
- Charges are arranged at the corners of a square of side length ‘a’.
- We want to find the electric potential at the center of the square.
Let’s denote the distance from each charge to the center of the square as 𝑟. Since it’s a square, all distances are equal.
The electric potential 𝑉 due to a point charge 𝑞 at a distance 𝑟 is given by Coulomb’s law:

Where:
- 𝑘 is Coulomb’s constant.
In this case, each charge is equidistant from the center of the square, so we can calculate the potential due to one charge and then multiply it by 4 (since there are four charges).
Given that the distance from each charge to the center is

(by considering the diagonal of the square), we can calculate the potential due to one charge:
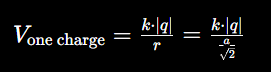
And the total potential at the center of the square is:

So, the electric potential at the center of the square due to the arrangement of charges is

In conclusion, the electric potential at the center of a square, formed by four identical charges of magnitude +𝑞 placed at its corners, is given by

, where 𝑘 is Coulomb’s constant and 𝑎a is the side length of the square. This result highlights the symmetry of the arrangement, where each charge contributes equally to the potential at the center. Understanding such configurations enhances our comprehension of electrostatic phenomena and their mathematical representations.
FAQ:
1. What is the electric potential in a square arrangement of charges?
- The electric potential in a square configuration of charges refers to the electrical potential energy per unit charge at a specific point within the square.
2. How are the charges arranged in the square configuration?
- Four identical charges, each denoted as +𝑞+q, are positioned at the corners of the square.
3. How is the electric potential calculated at the center of the square?
- The electric potential at the center of the square is determined by summing up the contributions from each charge using Coulomb’s law, considering the distances between the charges and the center.
4. What is the formula for the electric potential in this scenario?
- The formula for the electric potential (𝑉totalVtotal) at the center of the square is given by 4𝑘𝑞2𝑎a4kq2, where 𝑘k represents Coulomb’s constant and 𝑎a is the side length of the square.
5. What does the calculated electric potential signify?
- The calculated electric potential demonstrates the symmetric distribution of charges and their collective influence on the electrical environment within the square configuration.
6. Why is understanding electric potential in such configurations important?
- Understanding the electric potential in square configurations of charges enhances comprehension of electrostatic interactions and aids in predicting and analyzing electrical phenomena in various systems.
7. How does this knowledge contribute to practical applications?
- Knowledge of electric potential in charge configurations facilitates the design and optimization of electrical systems, including circuits, sensors, and electronic devices, by providing insights into charge distribution and behavior.
8. Are there any implications for fields beyond electromagnetism?
- Yes, concepts related to electric potential in charge configurations have applications in fields such as physics, engineering, and materials science, influencing research and technological advancements in diverse areas.